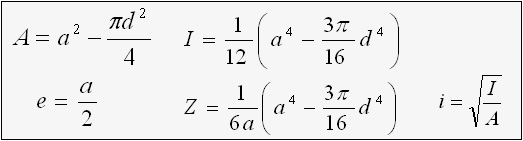Cross Section

A：Area （Units²）
e：Extreme point（Units）

I：Moment of Inertia（Units⁴）
Z：Section Modulus（Units³） →　I/e
i：Radius of Gyration（Units）　→ √（I/A）

Regular Hexagon

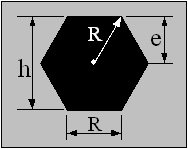
A = 3√3 ・　R² / 2

e = h/2

Z = 5 R³ /8

i = √(5/24)　・R = 0.457R

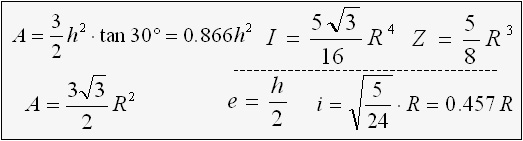
Regular Hexagon

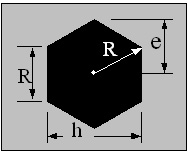
A = 3√3 ・　R² / 2

e = 0.577h　＝　R

Z = 5√3 ・　R³ /16

i =  √(5/24)　・　R = 0.457R

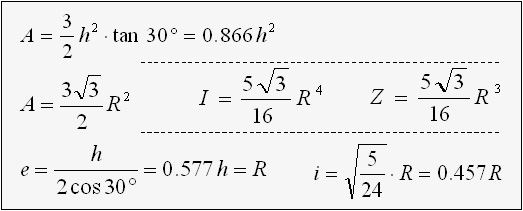
Trapezoid

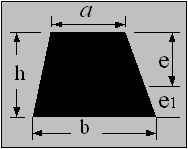
e = h・( a + 2b ) / ( 3 ( a + b ) )

Z = h² ( a² + 4 ab + b² )/ ( 12 ( a + 2b ) )

i = √(h² (a² + 4ab + b²)/ (18 (a + b)² ) )

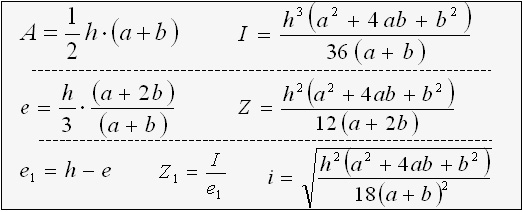
Triangle

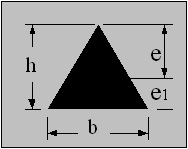
e = 2h / 3

Z = b h² / 24

i = √( h / 18 )    = 0.236 h  

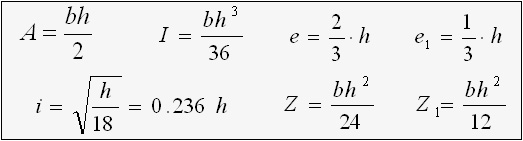
Half Round

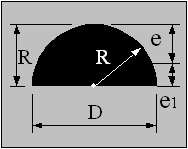
e = D (3π- 4) / ( 6π)

Z = D³ ・( 9π² - 64) / ( 192 (3π-4))

i = √( D² ( 9π² - 64) / (144π) )   

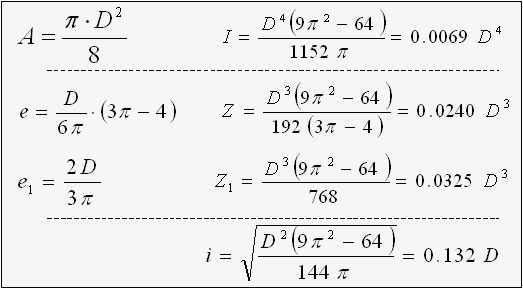
Half Round−Stand

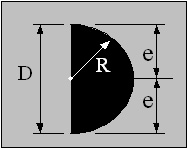
e = R

Z = π R³ / 8

i = R / 2

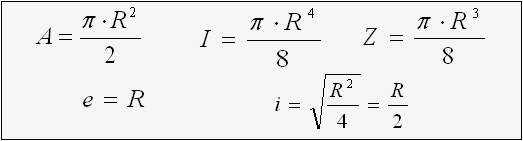
Oval

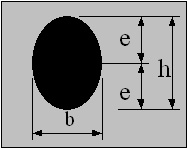
e = h / 2

Z = π b h²  / 32

i = h / 4

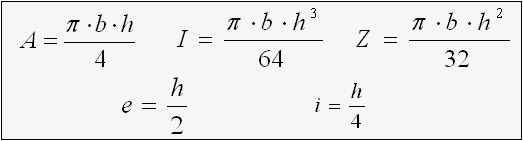
Half Round Tube / Pipe

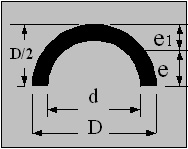
e = 2 ( D³ - d³ )/(3π( D² - d² ))

Z = I / e

i = √ ( I/A )

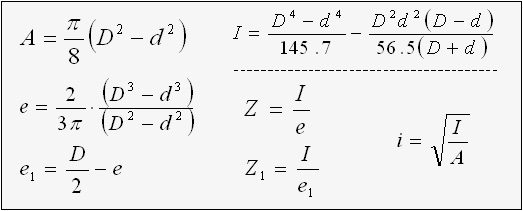
Oval Tube / Pipe

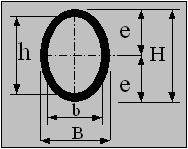
e = H / 2

Z = π( BH³ - bh³ ) / ( 32H )

i = √( (BH³ - bh³ ) / (16( BH - bh) ) )

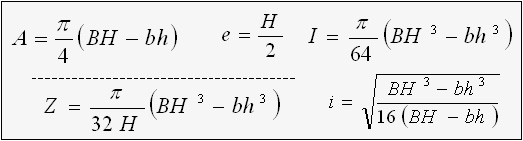
Square and Round Hole

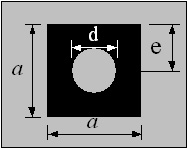
e = a / 2

Z = ( a⁴ - 3πd⁴ / 16) / ( 6a )

i = √ ( I/A )