潮汐力

index → 物理学ハンドブック      公式集  （物理）            ＊＊

  月の公転周期と自転周期がなぜ同じなのか

その原因は、地球と月との間で働く潮汐作用が関係しています。

では、なぜ、そうなるのか考えてみます。

そもそも潮汐力とは、

潮汐力

物体に働く重力の差によって、その物体を引き伸ばす力

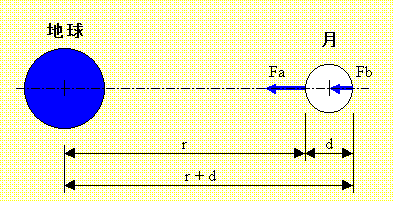
地球の中心から月までの距離を考えると、

月の地球側に最も近い点に働く重力 Fa と

地球側から最も遠い点に働く重力 Fb との差が潮汐力となる。

よって、月はごくわずかながら、ゆがんだ形になろうとする。

潮汐力の大きさは、差の計算なので それぞれの 万有引力 を計算すると

Fa − Fb ＝ G M ｍ ／ r ² −  G M ｍ ／ ( r + d )  ² となる。

　

  月の引力による地球への影響を考えると

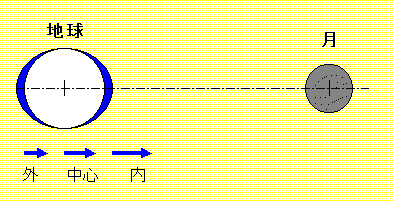
月の引力は、月に面した内側が最も大きく、反対側の外側は最も小さい。また、中心はその中間の引力となり、地球はゆがんだ形になろうとする。

地球には、海があり、固体に比べ液体は自由に形を変えられるので、海水が膨らんで潮の満ち引きが起こる。

地球そのものも潮汐力によってわずかにゆがむが、固体なのでごくわずかである。

　

では、月の公転周期と自転周期がなぜ同じなのか

もう一度、地球の引力によって月が受ける潮汐力を考えてみると

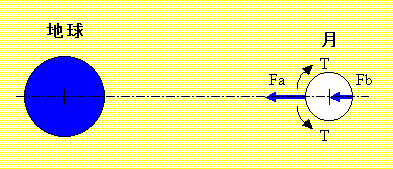
常に、Fa の引力が大きいので、月が回転（自転）する力を押えようとして、月のぶれをなくそうとする。
つまり、月は同じ面を地球に向けようとする力が働くことになる。実際は、月は地球の回りを回っているので、地球の回りを１回転すると、ちょうど月が１回転自転したことになる。

　

月の誕生直後は、自転速度が早かった。

誕生直後は、いまよりずっと地球の近くを回っており、自転速度も非常に早かったと考えられている。しかし、月に働く潮汐力が強大であったため、月の内部では物質が常にかき乱され、激しい摩擦力が生じた。そして、この摩擦力がブレーキとなって月の自転がしだいに遅くなり、現在のように安定した。

同じような太陽系の衛星

木星の４大衛星（カリスト、ガニメテ、エウロパ、イオ）
土星の衛星（タイタン）

これらも、月と同じ公転周期と自転周期が完全一致している。

丶 jin 丶